Q14: For the given points of two classes red and blue:Blue: { (1,2), (2,1), (1,-1), (1,-2)}Red : { (3,1), (4,3), (3,5), (6,3)}Plot a graph for the red and blue categories. Find the support vectors and optimal separating line.

Q14: For the given points of two classes red and blue:
Blue: { (1,2), (2,1), (1,-1), (1,-2)}
Red : { (3,1), (4,3), (3,5), (6,3)}
Plot a graph for the red and blue categories. Find the support vectors and optimal
separating line.

Given
Blue class B={(1,2),(2,1),(1,−1),(1,−2)}B = \{(1,2), (2,1), (1,-1), (1,-2)\}B={(1,2),(2,1),(1,−1),(1,−2)}
Red class R={(3,1),(4,3),(3,5),(6,3)}R = \{(3,1), (4,3), (3,5), (6,3)\}R={(3,1),(4,3),(3,5),(6,3)}

1) Plot (description)

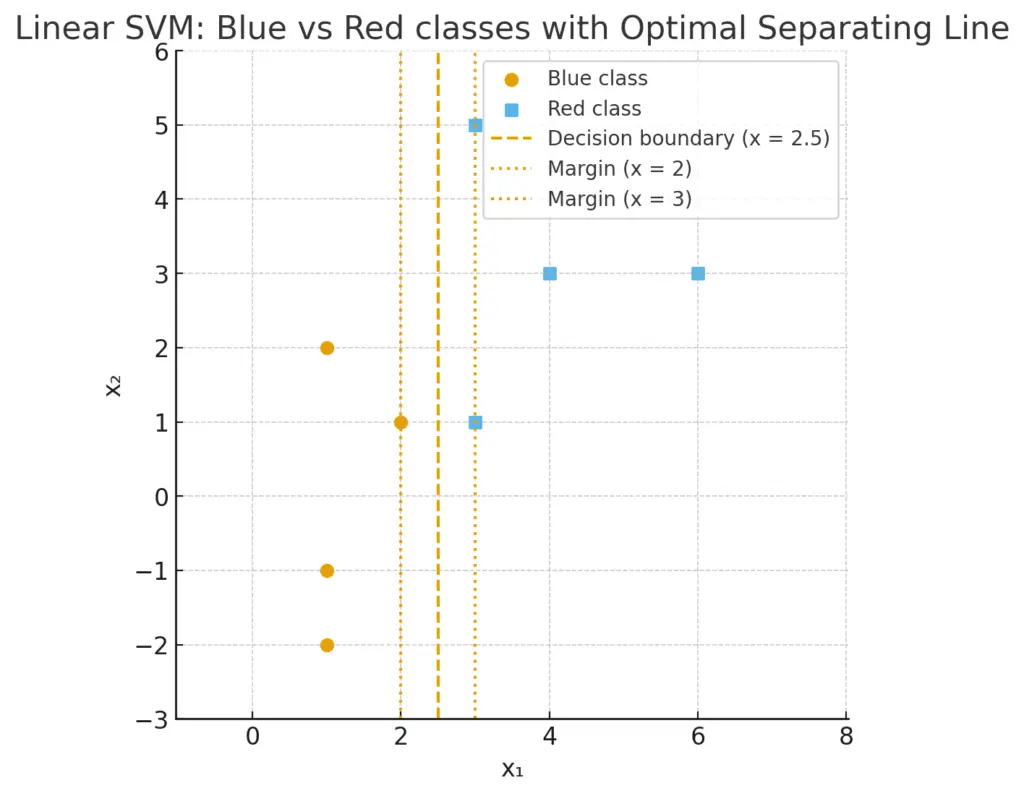
If we plot the points on the (x1,x2)(x_1,x_2)(x1,x2)-plane:

All blue points have x1≤2x_1 \le 2×1≤2; in fact the closest blue point to the red class in the x1x_1x1-direction is (2,1)(2,1)(2,1).
The red points lie to the right; the closest red points to the blue class are those with x1=3x_1=3×1=3, namely (3,1)(3,1)(3,1) and (3,5)(3,5)(3,5).

This clear left–right separation suggests a vertical separating line.

(An illustrative graph with classes, the optimal line, and margins is provided above: boundary at x1=2.5x_1=2.5×1=2.5, margins at x1=2x_1=2×1=2 and x1=3x_1=3×1=3.)

2) Linear separability and margin geometry

Because the nearest opposing points in the horizontal direction sit at x1=2x_1=2×1=2 (blue) and x1=3x_1=3×1=3 (red), the maximum-margin hyperplane in R2\mathbb{R}^2R2 is the vertical line exactly halfway between them: x1=2.5 \boxed{\,x_1 = 2.5\,}x1=2.5

The two margin lines (distance 1/21/21/2 on either side of the boundary) are: x1=2andx1=3 \boxed{\,x_1 = 2 \quad \text{and} \quad x_1 = 3\,}x1=2andx1=3

3) Support vectors

Support vectors are the training points that lie exactly on the margin lines:

Blue support vector(s): points with x1=2x_1=2×1=2
⇒ (2,1)\;\;\Rightarrow\;\; \boxed{(2,1)}⇒(2,1)
Red support vector(s): points with x1=3x_1=3×1=3
⇒ (3,1), (3,5)\;\;\Rightarrow\;\; \boxed{(3,1),\ (3,5)}⇒(3,1), (3,5)

These three points touch the margin lines and determine the maximum-margin separator.

4) Optimal separating line (SVM form)

A convenient parameterization of the optimal hyperplane is: w=(2, 0),b=−5\mathbf{w} = (2,\,0), \qquad b = -5w=(2,0),b=−5

The decision function is: f(x) = w⋅x+b = 2×1−5f(\mathbf{x}) \;=\; \mathbf{w}\cdot \mathbf{x} + b \;=\; 2x_1 – 5f(x)=w⋅x+b=2×1−5

Decision boundary f(x)=0 ⟺ 2×1−5=0 ⟺ x1=2.5f(\mathbf{x})=0 \iff 2x_1 – 5 = 0 \iff \boxed{x_1=2.5}f(x)=0⟺2×1−5=0⟺x1=2.5.
Margins f(x)=±1⇒x1=2 and 3f(\mathbf{x})=\pm 1 \Rightarrow x_1 = 2\ \text{and}\ 3f(x)=±1⇒x1=2 and 3 as above.
Classification rule: predict Red if f(x)>0f(\mathbf{x})>0f(x)>0 (i.e., x1>2.5x_1>2.5×1>2.5); predict Blue if f(x)<0f(\mathbf{x})<0f(x)<0 (i.e., x1<2.5x_1<2.5×1<2.5).

5) Margin width

Under the standard hard-margin SVM constraints yi(w⋅xi+b)≥1y_i(\mathbf{w}\cdot \mathbf{x}_i+b)\ge 1yi(w⋅xi+b)≥1, the geometric margin on each side is: γ = 1∥w∥ = 122+02 = 12 = 0.5\gamma \;=\; \frac{1}{\lVert \mathbf{w}\rVert} \;=\; \frac{1}{\sqrt{2^2+0^2}} \;=\; \frac{1}{2} \;=\; 0.5γ=∥w∥1=22+021=21=0.5

Hence the total margin width (distance between the two margin lines) is: 2γ=1\boxed{2\gamma = 1}2γ=1

which matches the horizontal gap between x1=2x_1=2×1=2 and x1=3x_1=3×1=3.

Final Answer (concise)

Support vectors: (2,1)\boxed{(2,1)}(2,1) from Blue; (3,1),(3,5)\boxed{(3,1), (3,5)}(3,1),(3,5) from Red.
Optimal separating line (maximum-margin): x1=2.5\boxed{x_1=2.5}x1=2.5 (vertical line).
SVM parameters (one valid choice): w=(2,0), b=−5\boxed{\mathbf{w}=(2,0),\ b=-5}w=(2,0), b=−5.
Margins: x1=2\boxed{x_1=2}x1=2 and x1=3\boxed{x_1=3}x1=3; total margin width =1=1=1.